文章目录

• 1. 问题描述
• 2. 问题分析
• 3. 算法设计
• • 🍑 动图演示
• 4. 程序设计
• 5. 流程框架
• 6. 代码实现
• 7. 问题拓展

---

1. 问题描述

对 N N N 个整数（数据由键盘输入）进行升序排列。

2. 问题分析

对于 N N N 个数因其类型相同，我们可利用 数组 进行存储。
 
冒泡排序是在 两个相邻元素之间进行比较交换的过程将一个无序表变成有序表。
 
冒泡排序的思想：首先，从表头开始往后扫描数组，在扫描过程中逐对比较相邻两个元素的大小。
 
若相邻两个元素中，前面的元素大于后面的元素，则将它们互换，称之为消去了一个逆序。
 
在扫描过程中，不断地将两相邻元素中的大者往后移动，最后就将数组中的最大者换到了表的最后，这正是数组中最大元素应有的位置。
 
然后，在剩下的数组元素中（n-1个元素），重复上面的过程，将次小元素放到倒数第 2 个位置。
 
不断重复上述过程，直到剩下的数组元素为 0 为止，此时的数组就变为了有序。
 
假设数组元素的个数为 n n n，在最坏情况下需要的比较总次数为: ( ( n − 1 ) + ( n − 2 ) + . . . + 2 + 1 ) = n ( n − 1 ) / 2 ((n-1)+(n-2)+...+2+1)=n(n-1)/2 ((n−1)+(n−2)+...+2+1)=n(n−1)/2。

3. 算法设计

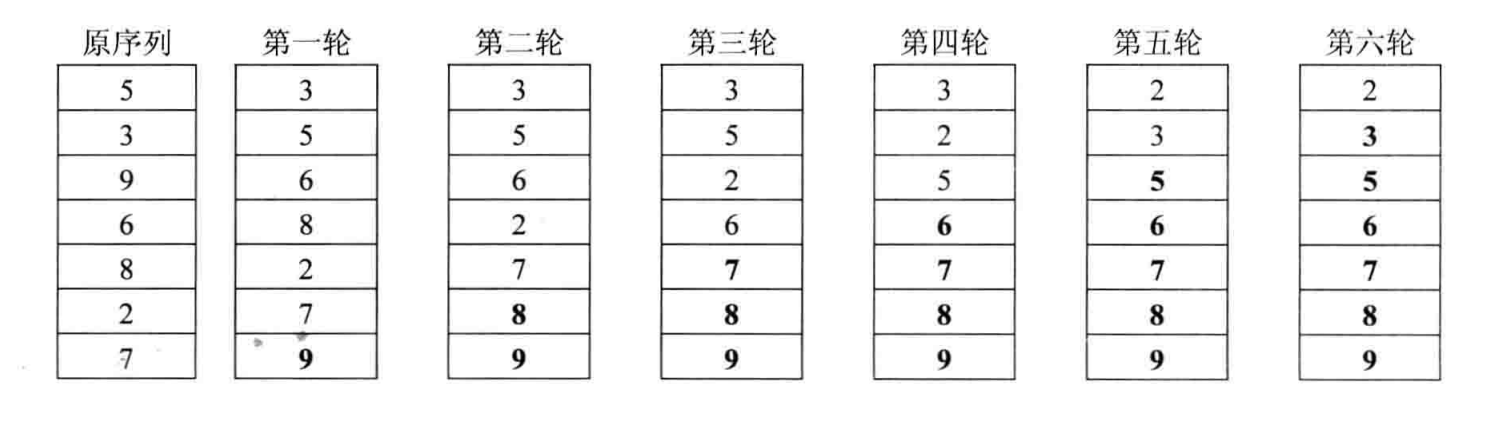
冒泡排序的过程我们用示意图简单的表示，从整个排序过程中寻找规律， n n n 个元素只需比较 n − 1 n-1 n−1 次即可。
 
假设一个数组中有 7 个元素，现在对这 7 个元素进行排序，只需比较 6 轮即可得到所要的有序序列。
 
示意图中最后加粗的数字即为经过一轮交换位置固定的数字。示意图如下：

🍑 动图演示

清楚了冒泡排序的过程，我们再来看一个动态图
 

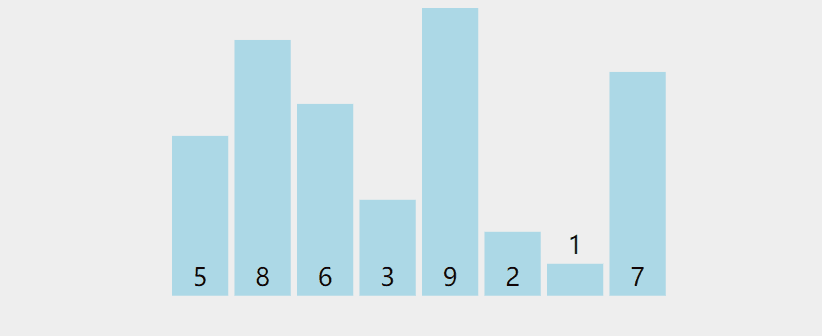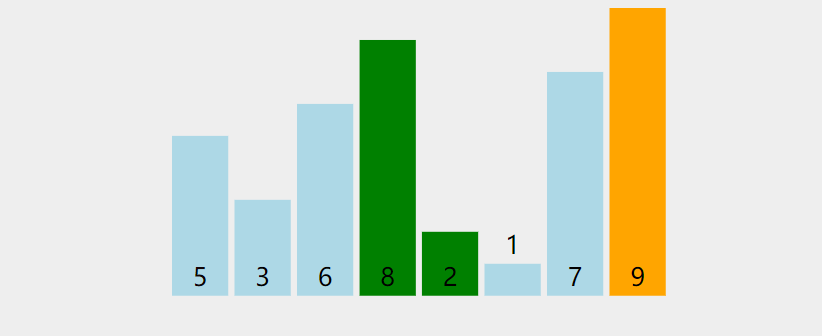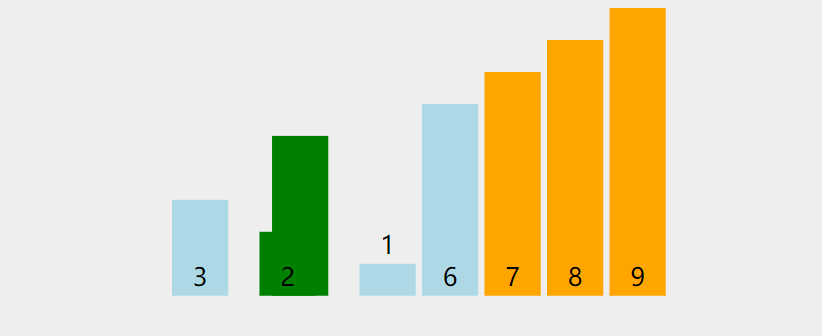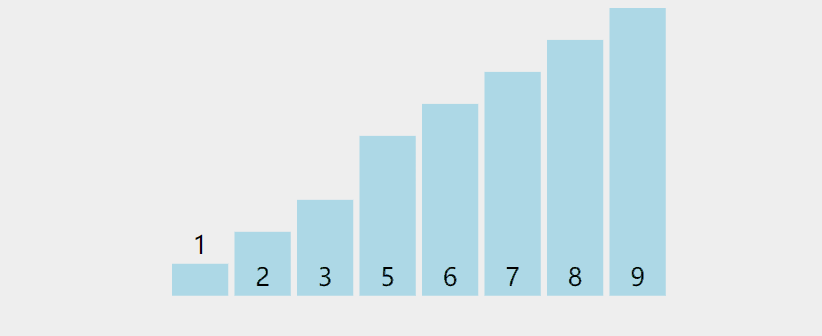
4. 程序设计

设计一👇

数组名用 a 表示、数组下标用 j 表示，数组中相邻两个元素的下标可表示为 a[j]、a[j+1] 或 a[j-1]、a[j]。
 
在利用数组解决问题时需要注意数组下标不要越界。
 
假如定义一个整形数组 int a[n]，则数组元素下标的取值范围是 0 ～ ( n − 1 ) 0～(n-1) 0～(n−1)，下标小于 0 0 0 或者大于 n − 1 n-1 n−1 都视为下标越界。
 
如果相邻元素采用 a[j]、a[j＋1] 表示的话，则下标取值范围是 0 ～ ( n − 2 ) 0～(n-2) 0～(n−2)；
 
若采用 a[j-1]、a[j] 表示，下标取值范围则是 1 ～ ( n − 1 ) 1～(n-1) 1～(n−1)

设计二👇

数组元素互换 也是经常遇到的一类题型，一般这种情况我们需要 借助一个中间变量 才可以完成，对于许多初学者来说经常犯的一个错误是：对两个元素直接相互赋值，而不借助中间变量。
 
我们先来看生活中的一个例子：
 
在蓝墨水瓶中装有蓝墨水，红墨水瓶中装有红墨水；现在我们要把蓝墨水放到红墨水瓶中，红墨水放到蓝墨水瓶中。
 
做法是先找一个白色空瓶（作用相当于程序中的中间变量）：
 
首先将蓝墨水倒入白色空瓶： t=a[i] 或 t=a[i+1]；
 
接着将红墨水倒入蓝墨水瓶：a[i]=a[i+1] 或 a[i+1]=a[i]；
 
最后将白瓶中的蓝墨水倒入红墨水瓶：a[i+1]=t 或 a[i]=t；
 
经过这 3 步就完成了红墨水与蓝墨水的互换。如果不借助白色空瓶，直接把蓝墨水倒入红墨水瓶，或把红墨水倒入蓝墨水瓶，这样必将破坏原来所存储的内容。
 

第一轮的交换过程可以用简单的程序段进行表示：

第二轮交换过程（最后一个元素经过第一轮比较已经确定，不需要再次进行比较）：

第三轮交换过程（最后两个元素已经确定，不需要再次进行比较）：

结论👇

由上面的程序段发现，第一轮比较的判定条件为 j < n-1；
 
第二轮为 j < n-2；
 
第三轮为 j < n-3；
 
依次类推，第 i 轮的循环判定条件必为 j < n-i。
 
在编程过程中我们可以用两层循环来控制，第一层循环控制交换的轮数，第二层循环控制每轮需要交换的次数。

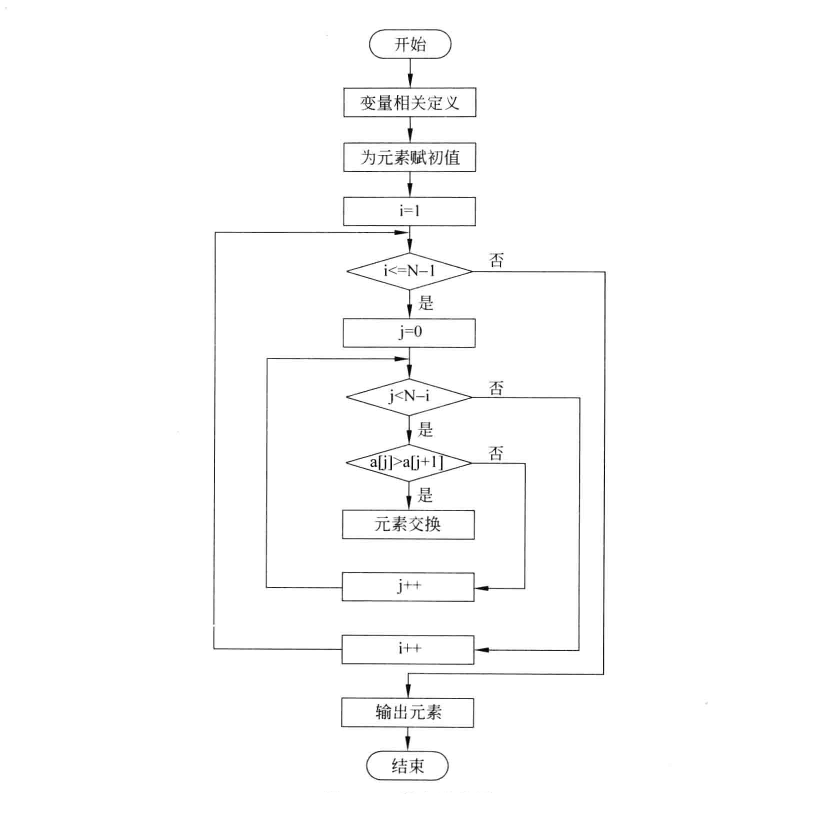
5. 流程框架

6. 代码实现

假设有下面一组无序数组，我们要对它进行升序排序

完整代码📝

#include <stdio.h>//冒泡排序函数void BubbleSort(int arr[], int len){	int i;	int j;	int temp;	for (i = 0; i < len - 1; i++) //控制比较的轮数	{		for (j = 0; j < len - 1 - i; j++) //控制每轮比较的次数		{			if (arr[j] > arr[j + 1]) //数组相邻两个元素进行交换			{				temp = arr[j];				arr[j] = arr[j + 1];				arr[j + 1] = temp;			}		}	}}//输出函数void print(int arr[], int len){	int i;	for (i = 0; i < len; i++)	{		printf("%3d ", arr[i]);	}}int main(){	int arr[10] = { 5,8,6,3,9,2,1,7,12,4 };	BubbleSort(arr, 10);	printf("The data after sorted：n");	print(arr, 10);	printf("n");	return 0;}

运行结果👇

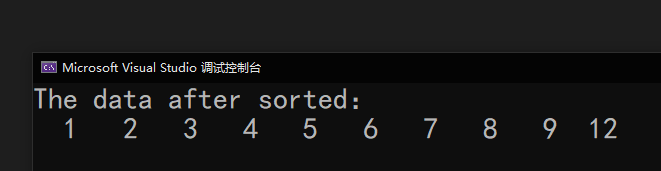
代码贴图👇

7. 问题拓展

常用的排序方法除了上述的冒泡排序外，还有选择排序、插入排序、快速排序和堆排序等，下面简单介绍一下 选择排序。
 
选择排序思想：
 
扫描整个线性表，第一轮比较拿数组中的第一个元素与其他元素进行比较，遇到比第一个元素小的则进行交换；
 
再拿着交换之后的第一个元素接着上次比较的位置与后面的元素进行比较，直到扫描到线性表的最后，从中选出最小的元素，将它交换到表的最前面（这是它应有的位置）。
 
第二轮比较的时候从第二个元素开始，依次与第三个、第四个直到最后一个比较，在比较过程中有比第二个元素小的进行交换，接着与后面的元素比较；
 
对剩下的子表采用同样的方法，直到子表为空。在最坏情况下需要比较 n ( n − 1 ) / 2 n(n-1) / 2 n(n−1)/2 次。

选择排序如下📝

#include <stdio.h>//选择排序void selectSort(int arr[], int len){	int i;	int j;	for (i = 0; i < len - 1; i++)	{		int min = i;//假设第一个元素是最小的		for (j = i + 1; j < len; j++)		{			if (arr[j] < arr[min])			{				min = j;//保存最小元素的下标			}		}		//交换		int temp = arr[min];		arr[min] = arr[i];		arr[i] = temp;	}}//输出void print(int arr[], int len){	for (int i = 0; i < len; i++)	{		printf("%3d ", arr[i]);	}}int main(){	int arr[10] = { 5,8,6,3,9,2,1,7,12,4 };	selectSort(arr, 10);	printf("The data after sorted：n");	print(arr, 10);	printf("n");	return 0;}

运行结果👇

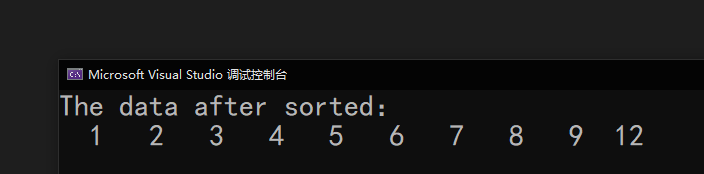
代码贴图👇

不同排序法的效率是不同的，不同需求情况下可选择不同的方法。

因为本篇文章是为了让初学者对排序有一个大概的认识，所以暂不考虑算法的复杂度以及优化。